计算机的运算方法

参考：https://blog.csdn.net/SX123q/article/details/124597298

无符号数特点：保存时只有数值位，没有符号位。假如使用寄存器保存无符号数，那么：寄存器的位数反映了无符号数的表示范围。例如：

• 寄存器为 8 位，无符号数表示范围为 0~255

• 寄存器为16位，无符号数表示范围为 0~65535

有符号数的机器数与真值

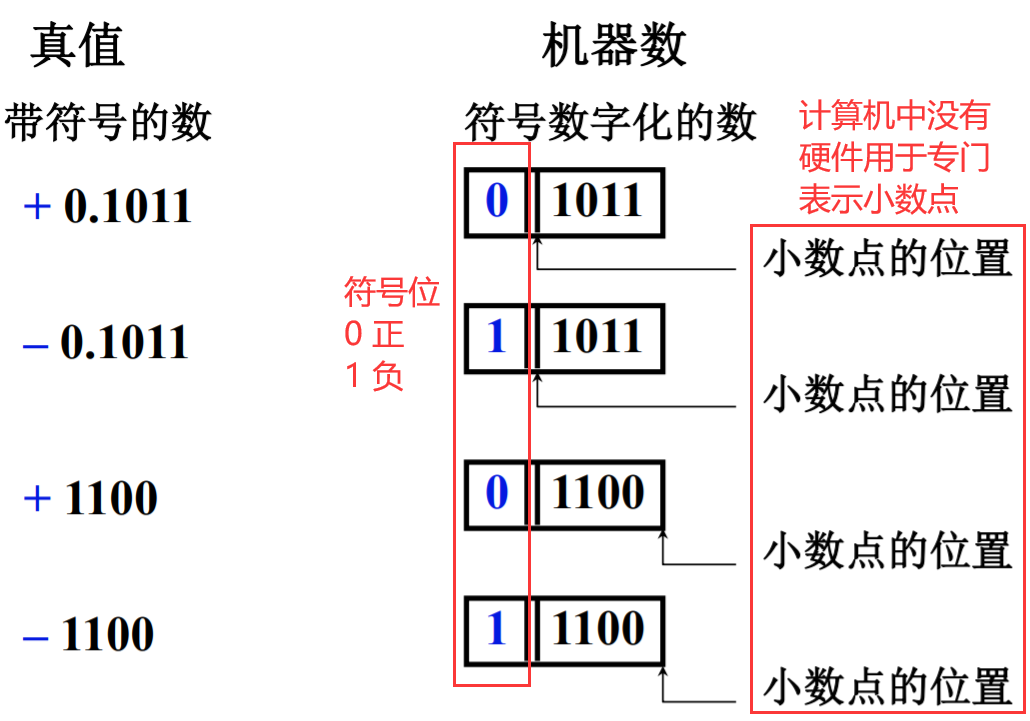
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为 0, 负数为 1

将带符号位的机器数对应的真正数值称为机器数的真值

机器数与真值

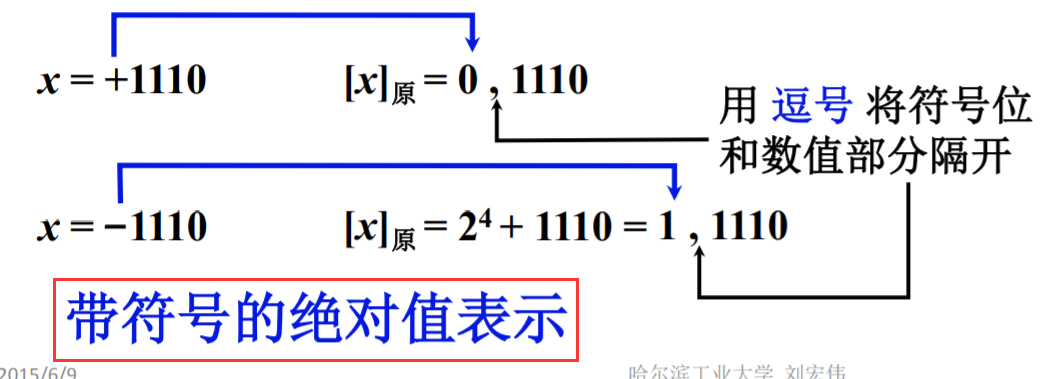
2. 原码表示法

整数定义如下：

$$\begin{cases} 0，x \qquad 2^n > x \geq 0 \\ 1，-x \quad 0 \geq x > -2^n \end{cases} \qquad x为真值，n为整数的位数$$

对于 $2^n-x$ 的解释：数值部分位数为 n，符号位如果加一的话，实际上就相当于给这个数据的绝对值加上了 $2^n$

整数的原码表示法

小数定义如下：

$$\begin{cases} x \qquad \quad 1>x \geq0 \\ 1-x \quad 0 \geq x > -1 \end{cases}$$

小数原码表示法

原码的特点：简单、直观。但是用原码有如下问题：

原码运算问题

例题

原码表示法例题

3. 补码表示法

什么时候-3和+9等价？ $-3 \equiv 9 ,(mod ,12)$ ，称+9是-3以12为模的补数。

在这里，我们通过模，实现了用一个正数代表一个负数，实现了用加法替换减法

这里有两个结论：

1. 一个负数加上“模”即得该负数的补数（正数）

2. 一个正数和一个负数互为补数时， 它们绝对值之和即为 “模” 数

以计数器阐释补数的概念

计数器阐释补数的概念

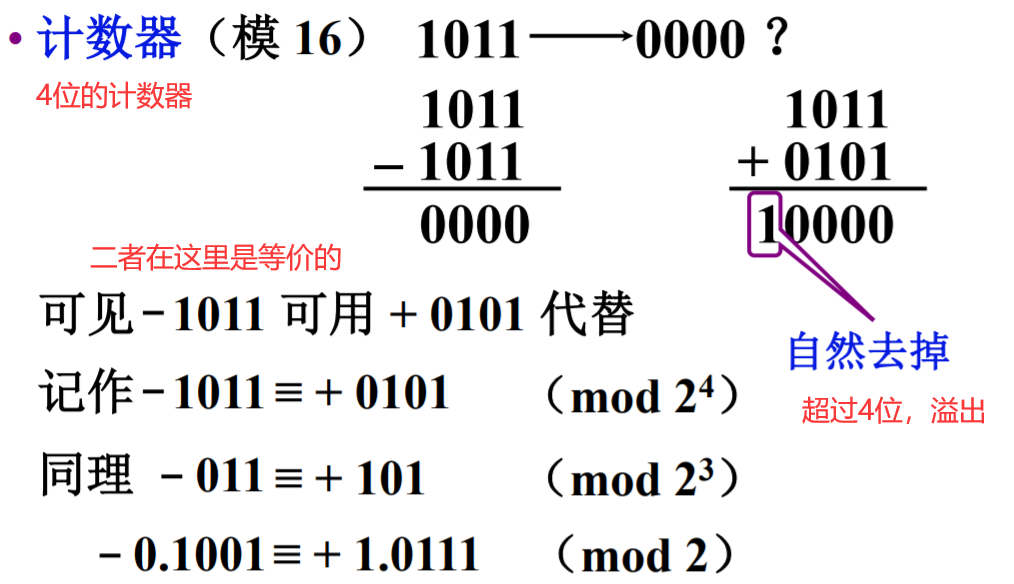
在这里介绍了补数计算公式的原理

公式原理

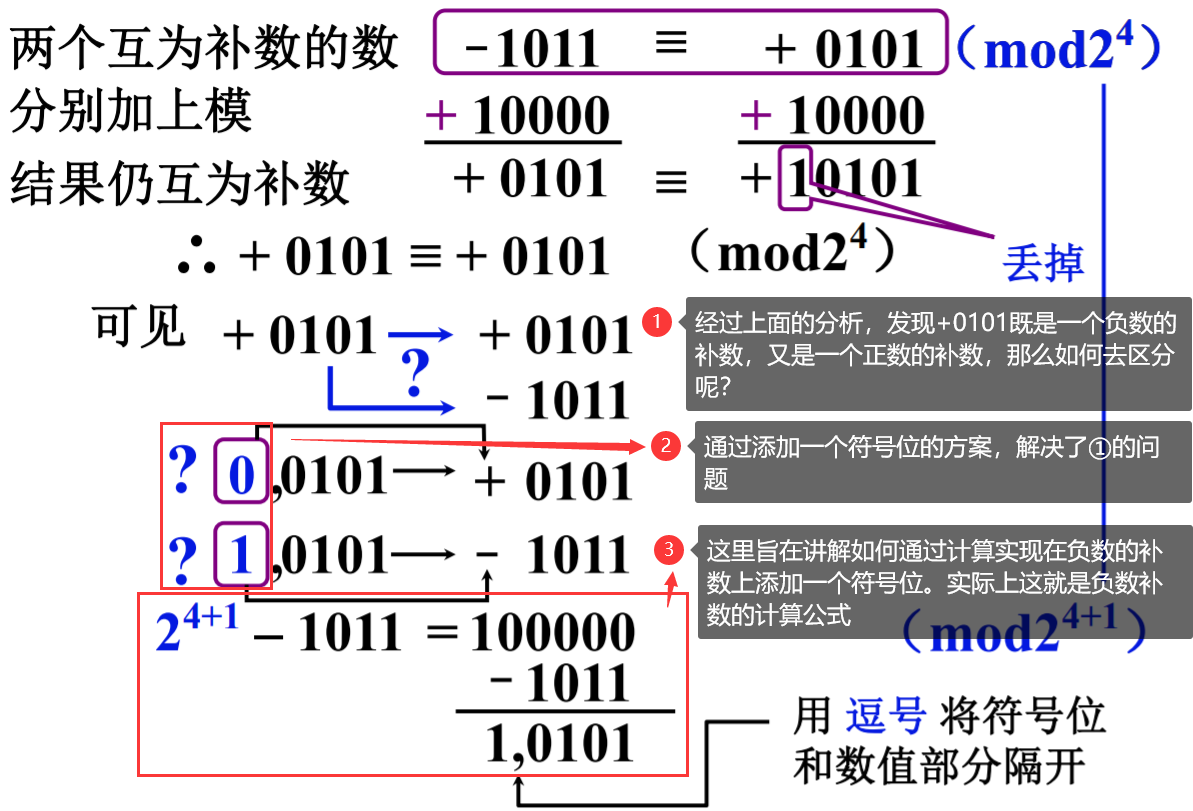
整数补码定义公式如下：

$$[x]_补= \begin{cases} 0，x \qquad 2^n>x\geq0 \\ 2^{n+1}+x \quad 0>x\geq -2^n \quad (\mod \, 2^{n+1}) \end{cases} \qquad x为真值，n为整数的位数$$

例子

小数公式如下：

$$[x]_补= \begin{cases} x \qquad 1>x\geq0 \\ 2+x \quad 0>x \geq-1 \quad (mod \, 2) \end{cases} \qquad x为真值$$

例子

当真值为负时，补码的快捷计算方法：

1. 转为原码

2. 除符号位外，其他每位取反

3. 取反后，末位+1

如图

例子

注意：补码定义公式是直接通过真值计算补码，而快捷求法是通过原码求补码

同时，当真值为负时，通过补码计算原码的方法：原码 可用 补码除符号位外 每位取反，末位加 1 求得

4. 反码表示法

反码整数定义

$$[x]_反= \begin{cases} 0，x \qquad\quad\quad\quad 2^n>x \geq 0 \\ (2^{n+1}-1)+x \quad 0 \geq x>-2^n \quad (mod \, 2^{n+1}-1) \end{cases} \qquad x为真值，n为整数的位数$$

反码整数例子

当真值为负数时，反码计算的快捷方式：原码除符号位外每位取反

小数

$$[x]_反=\begin{cases} x \qquad\quad\quad 1>x \geq 0 \\ (2-2^{-n}+x) \quad 0 \geq x>-1 \quad (mod \, 2-2^{-n}) \end{cases} \qquad x为真值，n为小数的位数$$

小数反码举例

反码例子

原码、补码、反码小结

1. 最高位为符号位，用指定符号将 数值部分 和 符号位 隔开

   • 整数用 ,

   • 小数用 .

2. 对于正数：

   • 原码 = 补码 = 反码

   • 真值变原码：最左侧加符号位 0

3. 对于负数，符号位为1，其数值部分

   • 原码除符号位外每位取反，末位+1 ----> 补码

   • 原码除符号位外每位取反 ----> 反码

补充一个小结论：二进制数，经过两轮取反末位+1操作，该二进制数是不变的。

例题

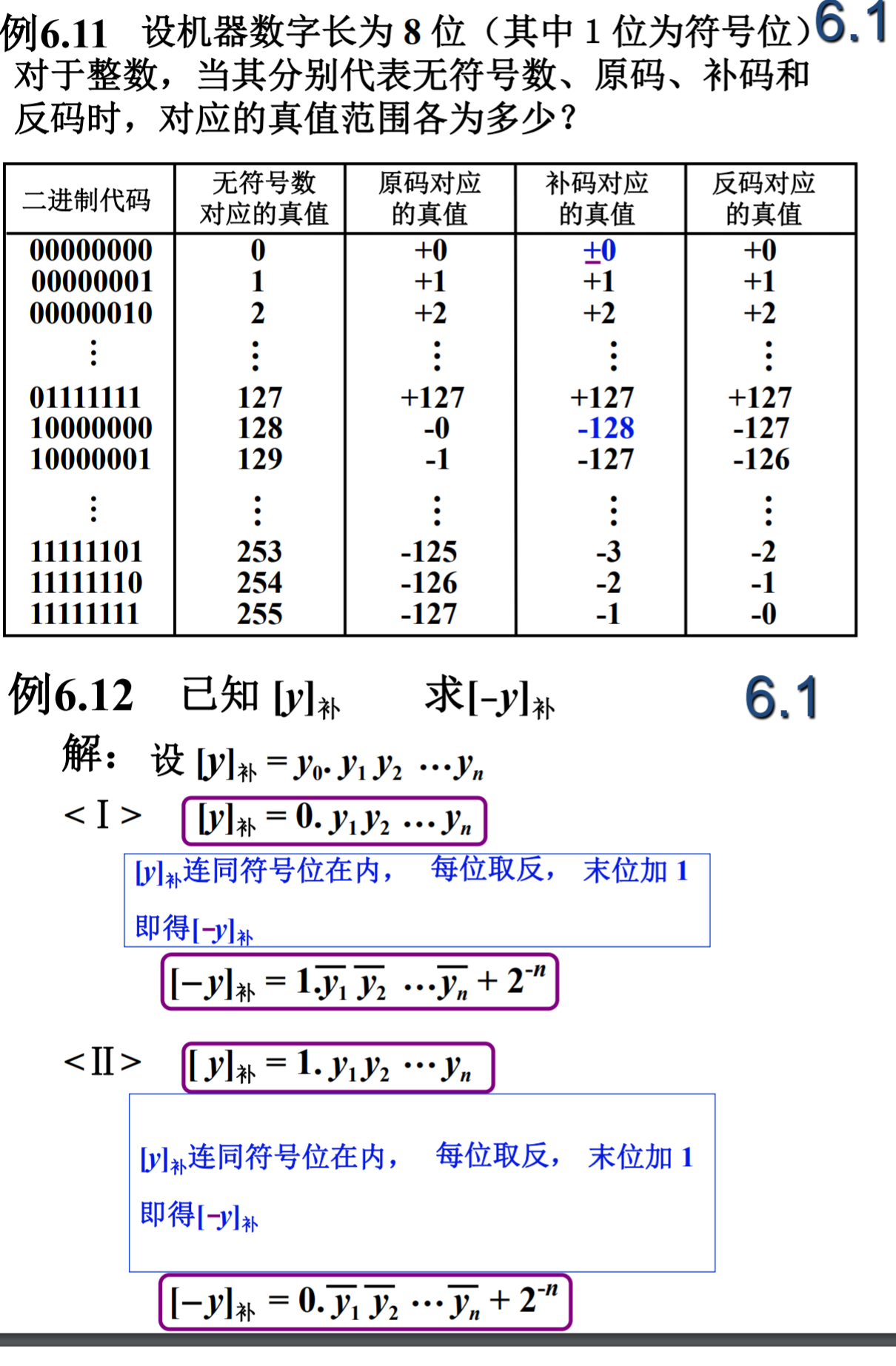
5. 移码表示法

为什么要采用移码？原因在于使用补码难以直接比较数的大小，如下图：

补码缺陷

公式如下：

$$x_移=2^n+x \quad (2^n>x \geq -2^n) \qquad x为真值，n为整数的位数$$

注意，移码只定义了整数。移码表示例子：

移码例子

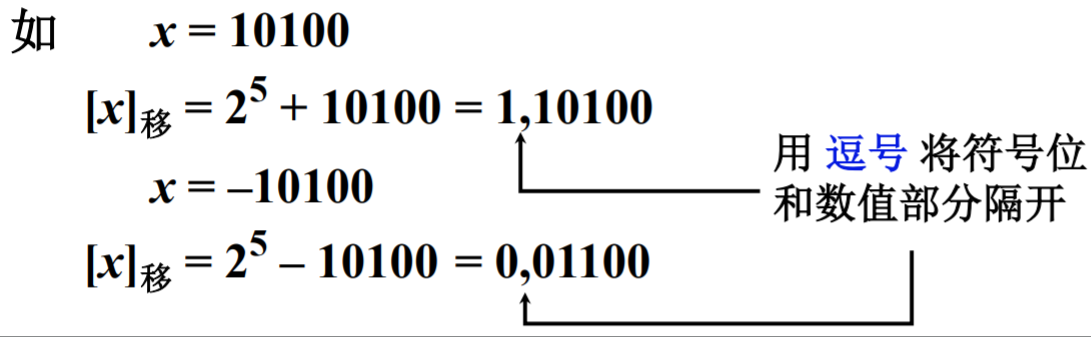
移码可以很方便的比较整数的大小，如下图：

移码比较大小

移码和补码的比较1

真值、补码和移码的对照表

真值、补码、移码对照表

移码的特点

• 用移码表示浮点数的阶码（整数），能方便地判断浮点数的阶码大小

• 即0的移码是唯一的：1,n个0

• 移码全0表示的是最小值 $-(2^{n-1})$ 全1时表示最大值 $2^{n-1}-1$如下图

示例

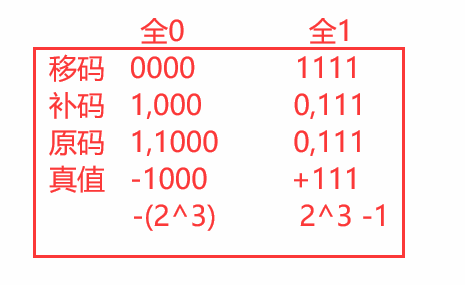
6. 数的定点表示和浮点表示

关于定点和浮点的概念

计算机中，没有为小数点设置专门的存储逻辑。小数点的位置是以约定的方式给出的。当约定小数点在某一指定点时，这就是定点表示。

依据约定小数点位置的不同，可以将计算机分成两种：小数定点机、整数定点机。如图

小数定点机和整数定点机

为什么在计算机中要引入浮点数表示？定点数表示所拥有的缺陷?

• 编程困难，程序员要调节小数点的位置

• 数的表示范围小，为了能表示两个大小相差很大的数据，需要很长的机器字长

• 数据存储单元的利用率往往很低

浮点数的一般形式

$$N=S \times r^j \qquad S\,尾数，j\,阶码，r\,尾数的基值$$

计算机中 r 取 2、4、8、16 等。如下例：

r=2

计算机中规定：（图中√标记的符合计算机要求）

1. 尾数S 取纯小数（可正可负），并称尾数最高位为1的浮点数为规格化数（这里最高位指的是尾数的真值部分，即小数点后第1位）

2. 阶码j 取整数（可正可负）

浮点数在计算机中的表示形式

浮点数在计算机中的表示形式

浮点数的表示范围

浮点数表示范围

练习题：

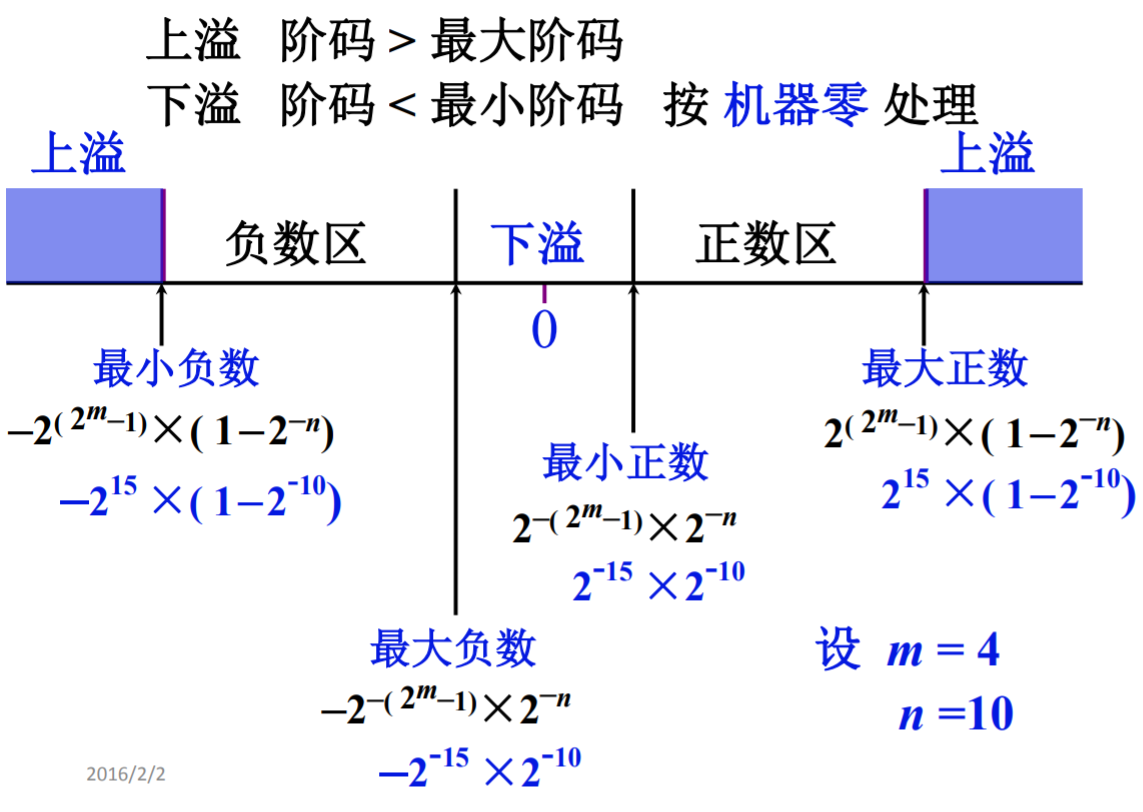
浮点数表示范围练习题

浮点数的规格化形式

基数r取值	规格化形式
2	尾数最高位为1
4	尾数最高 2 位不全为 0（2 个二进制位表示 1 个四进制位）
8	尾数最高 3 位不全为 0 （3 个 二进制位表示 1 个四进制位）

结论：基数不同，浮点数的规格化形式不同

浮点数的规格化

浮点数规格化的步骤：

1. 尾数左移或后移，使尾数的最高几位满足规格化形式的要求

   • 尾数左移：左规（数据相对小数点向左移动）

   • 尾数右移：右规（数据相对小数点向右移动）

2. 对阶码进行加减处理，使浮点数的真值不发生变化

如下示例：

浮点数的规格化

规格化范围计算例题

规格化范围计算例题

需要注意到：规格化后浮点数的范围和未规格化浮点数的范围是不同的

机器零

机器零

7. IEEE 754 标准

该标准规定浮点数在计算机中的表示形式为：

IEEE754标准

该标准同时要求：尾数必须采用规格化表示。特点如下：

• 尾数最高位必为1

• 只有一个小数点位置，它就是阶码的小数点位置，同时也是尾数的小数点位置

• 阶码为整数、尾数为纯小数

数值类型	符号位S	阶码	尾数	总位数
短实数	1	8	23	32
长实数	1	11	52	64
临时实数	1	15	64	80

8. 移位运算

如： 15.m = 1500.cm，相当于小数点右移两位。由于在计算机中小数点是按约定位置的，因此实际上小数点是不移动的。这种情况，我们称为：15 相对小数点左移两位（机器用语）

• 左移：绝对值扩大

• 右移：绝对值缩小

在计算机中，移位与加减配合，能够实现乘除运算

移位前提规则：符号位不变。移位添补规则如下：

移位添补规则

1. 正数移位运算

正数移位运算实例1

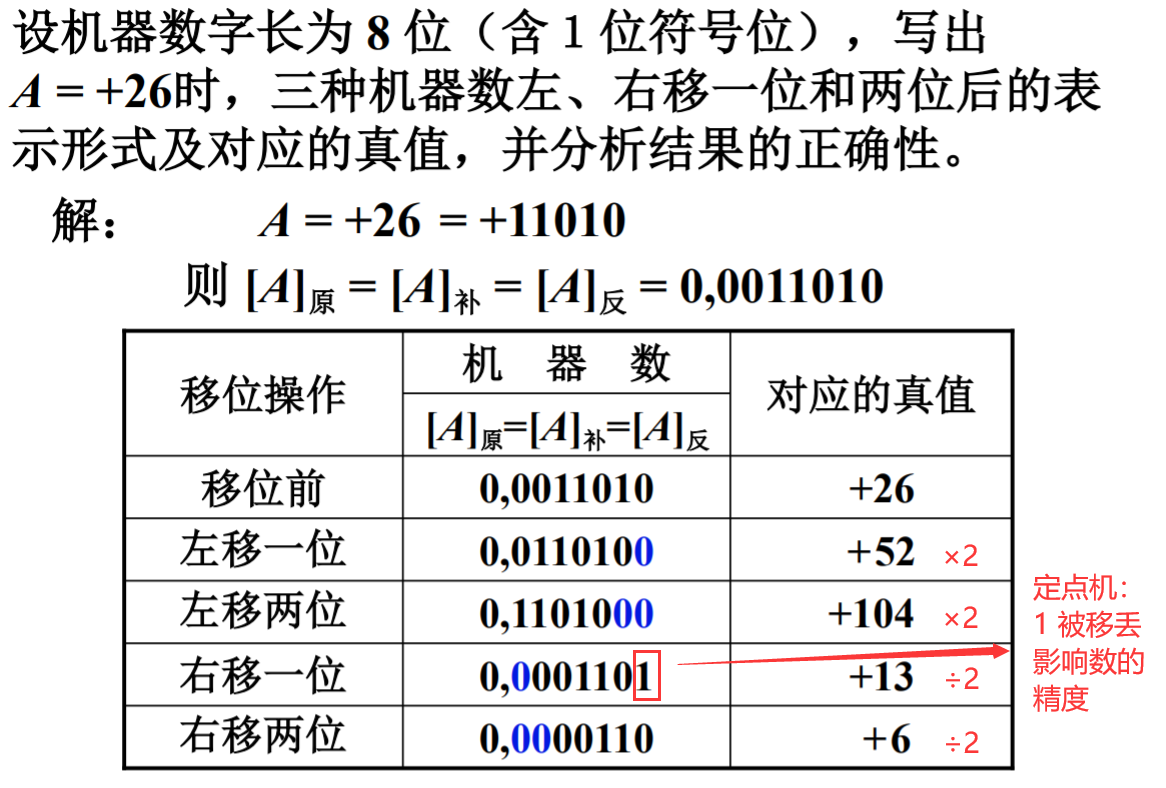
结论：对于正数的移位运算，无论是原码、补码还是反码

• 左移：相当于真值×2

• 右移：相当于真值÷2

这里还有一个非常重要的结论：在移位运算中（这里☞低位丢失）

1. 如果移位丢失的数位对应真值中的0，数的精度不会发生变化

2. 如果移位丢失的数位对应真值中的1，数的精度会发生变化

低位丢失影响精度，高位丢失改变数的大小（出错）

在接下来的负数移位运算例子中，请着重关注移位丢失对数的精度造成的影响

2. 负数移位运算

负数移位运算实例1

当精度丢失时，补码、反码对应的原码和真值移位对应的原码就有差别了。

同时，将本例中反码左移三位，会发现运算结果出错。原因在于反码左移3位时丢失了一个高位0，而这个高位0对应真值中的高位1。

3. 算术移位的硬件实现

如图

算术移位的硬件实现

4. 算术移位和逻辑移位的区别

算数移位和逻辑移位的区别

9. 加减法运算

为什么不使用原码进行运算？

因为在前面的介绍中，我们知道使用原码进行加减法运算，需要根据数的符号判别到底是加法运算还是减法运算，实现复杂

加法运算公式

$$整数 \qquad [A]_补+[B]_补=[A+B]_补 \, (\mod \, 2^{n+1})\\ 小数 \qquad [A]_补+[B]_补=[A+B]_补 \, (\mod \, 2)\quad$$

减法运算公式 A−B=A+(−B)

$$整数 \quad [A-B]_补=[A+(-B)]_补=[A]_补+[-B]_补 \, (mod\, 2^{n+1})\\ 小数 \quad [A-B]_补=[A+(-B)]_补=[A]_补+[-B]_补 \, (mod \, 2)$$

结论：在补码加减法运算中，实际上都是进行的加法。需要注意，连同符号位一起相加，符号位产生的进位自然丢掉

需要注意到这两个例子中，关于机器数指定部分。（实际运算一定要考虑机器数长度）下为例1

补码加减法例1

例2

补码加减法例2

一个例子引出溢出的概念

溢出例子

• 练习一出错原因：纯小数定点机，运算结果>1，发生溢出

• 练习二出错原因：8位整数定点机，表示范围在 -128 ~ +127，运算结果超出了这个范围，产生溢出

溢出的概念：数据长度超出机器字长。（也可以说是，数据超过了机器所能表示数字的范围）

一位符号位判溢出

判别方法：参与操作的两个数符号相同，其结果的符号与原操作数的符号不同，即为溢出。

分三种情况进行分析这个方法的正确性：

1. 两个数异符号：即符号为一正一负，既然这两个数能够在定点机中表示，它们本身是不会溢出的，那么经过运算，结果肯定也不会溢出。

2. 同为正数：假如运算结果变为负号，那就是发生了溢出。参考上面 练习一

3. 同为负数：加入运算结果变为正号，那就是发生了溢出。参考上面 练习二（练习二可以看成是两个负数相加）

两位符号位判溢出

首先需要明确：两位符号位 代表 以4为模

补充一个知识：假如以$2^k$为模，那么符号位就是k个。符号位有k个1或0，真值部分不变）

判别原理：

两位符号位判溢出原理

10. 乘法运算

实现

1. 分析笔算乘法

笔算乘法分析

计算机如何实现笔算乘法的四个要点

1. 符号位单独处理：采用一个异或电路对符号进行处理

2. 乘数的某一位决定是否加被乘数：将乘数放在移位寄存器中，每判断一次最低位，乘数右移一位（最低位丢失）

3. 4个位积一起相加：用一个寄存器进行累加操作

4. 乘积的位数扩大一倍：用两个寄存器一起保存乘积

2. 笔算乘法改进

笔算乘法改进

3. 改进后的笔算乘法过程（竖式）

如图 要注意：符号位是单独另外考虑的，这里只涉及数据位的计算。（整体移位的原因）

改进后的笔算乘法分析

改进算法步骤分析

1. 部分积初始值为 0

2. 根据乘数末位的值判断部分积加值，结果记为 X

   • 乘数末位为1，部分积 + 被乘数

   • 乘数末位为0，部分积 + 0

3. 将 2. 的结果X右移一位，形成新的部分积

4. 乘数右移一位，末位移丢（因为末位判断过了，要判断倒数第二位的值了）。

5. 从 2. 开始循环，直到乘数全部判断完成

注意：

1. 每一轮循环执行了两次移位，X移位一次，乘数移位一次

2. X移位时丢出来的低位数据，放在了乘数移位空出来的高位位置

3. 这里用到了3个寄存器，有2个分别保存部分积高位和乘数(和部分积低位)，具有移位功能。1个用于保存被乘数，不具有移位功能

4. 当计算完成后，两个寄存器合起来才是结果。其中：

   • 部分积寄存器保存结果的高位部分

   • 乘数寄存器保存结果的低位部分

4. 小结

1. 乘法 运算可用 加和移位实现。n位数据的乘法运算，需要n次加法运算和n次移位运算。n指运算数数据部分长度

2. 由乘数的末位决定被乘数是否与原部分积相加， 然后 右移1位 形成新的部分积，同时 乘数 右移1 位 （末位移丢），空出高位存放部分积的低位。

3. 被乘数只与部分积的高位相加

4. 硬件：3个寄存器（其中两个有移位功能），1个全加器（n+1位，实现相加操作）

原码乘

1. 原码一位乘运算规则

如图

原码1位乘运算规则

2. 原码一位乘递推公式

如图 其实和改进后的笔算乘法思想一致，那里看懂，这个就不会有问题

以下为例题

原码1位乘例题

特点：

1. 绝对值运算

2. 用移位的次数判断乘法是否结束

3. 逻辑移位

11. 除法运算

实现

如图

分析笔算除法

2. 笔算除法和机器除法的比较

实际上指明了机器运算如何实现笔算运算中的要点

笔算除法和机器除法的比较

需要注意的点：

1. x 在第一次计算时，是被除数。从第二次开始，代表的就是余数了。而y始终代表除数。看恢复余数法中的例子

2. 余数左移一位 和 除数右移一位 相对而言是等价的

3. 使用1倍字长加法器原因：用余数左移一位代替除数右移一位后，不会产生更多的位数

原码除法

基本原理

原码除法原理

计算机中除法运算的实现有两种：恢复余数法、不恢复余数法（加减交替法）。

1. 恢复余数法

假如求 [ x y ] 原 [\frac{x}{y}]_原 [yx]原，算法步骤：

1. 被除数和除数进行比较，判断商值。计算机通过补码减法运算判断： [ x ∗ ] 补 − [ y ∗ ] 补 = [ x ∗ ] 补 + [ − y ∗ ] 补 x ∗ , y ∗ 代 表 绝 对 值 [x^]_补-[y]_补=[x^]_补+[-y]_补 \qquad x^*,y^*代表绝对值 [x∗]补−[y∗]补=[x∗]补+[−y∗]补x∗,y∗代表绝对值

   • 余数为正数，上商为1，余数为x (x的值变了)

   • 余数为负数，上商为0 同时恢复被除数 x（上商为1代表这步减法是合规的，上商为0代表这里不能做减法，因此要恢复）

   • 注意： [ x ∗ ] 原 = [ x ∗ ] 补 = [ x ∗ ] 反 [x^]_原=[x^]_补=[x^*]_反 [x∗]原=[x∗]补=[x∗]反。

2. x 逻辑左移1位成为新的被除数。从第1步开始循环

特点：

1. x 代表的值一直在变化（做减法、做移位），而 y 代表的值是不发生变化的

2. x 从第二步开始就代表了余数（左移1位后成为新一轮除法运算的被除数），因为x可能会被恢复，因此这种方法名为 恢复余数法

3. 每一轮循环都会移位一次。n位的被除数，共移位n次

特点：

1. 上商 n+1 次

2. 第一次上商判溢出

3. 移位 n 次，加法 n+1 次

4. 用移位的次数判断除法是否结束

关于第一次上商判溢出

在纯小数定点机中，假如第一次上商为1，代表结果>1，产生了溢出。

恢复余数法运算规则：

恢复余数法运算规则

2. 不恢复余数法（加减交替法）

不恢复余数法运算规则（注意对比恢复余数法运算规则。实际上这个运算规则就是从恢复余数法运算规则中推导出来的）

不恢复余数法运算规则

特点：

1. 上商 n+1 次

2. 第一次上商判溢出

3. 移n次，加 n+1 次

4. 用移位的次数判断除法是否结束

12. 浮点四则运算

设 $x=S_x·2^{j_x} \quad y=S_y·2^{j_y}$

这里符号位使用两位，符号最高位是真正的符号位，在移位运算时，只有符号最高位不参与移位（算术移位）

为什么要对阶以及什么是对阶？

浮点数运算有两个前提要求：

1. 基值相同

2. 阶码相同

只有满足这两个要求，才能保证尾数进行加减法运算结果的正确性。而在基值相同的情况下，调整阶码使阶码相同就是对阶。对阶时尾数也要调整（保证真值不变）

计算机中，通过对阶码进行补码减法运算，判断阶差，并对阶码进行调整。下图给出了阶差公式及所有的调整方案：

求阶差

这里的 加减法、移位操作，操作数可以从 1 改为 Δ j

计算机采用的对阶原则是：小阶向大阶看起。原因：高位丢失影响大小，低位丢失影响精度。

对阶例子

3. 规格化

$$通用定义：\frac{1}{r}\leq|S|<1 \qquad r代表基值 \\ 当\,r=2\,时：\frac{1}{2}\leq|S|<1 \qquad$$

规格化数的判断

特例如下：

特例

左规，机器数采用补码：尾数左移一位（算数移位），阶码减 1，直到数符和第一数位不同为止。

对阶例题

右规，使用条件：当 尾数溢出（ >1）时，需 右规。即尾数出现 01. ×× …×或 10. ×× …×时

机器数采用补码：尾数右移一位（算术移位），阶码加 1

4. 舍入

在 对阶 和 右规 过程中，可能出现 尾数末位丢失 引起误差，需考虑舍入。两种舍入方案：

1. 0舍1入法：

   • 末位丢失0：不做处理

   • 末位丢失1：末位+1

2. 恒置1法：无论末位丢失0或1，始终把末位设为1

5. 溢出判断

首先要明确：这里的溢出是指整个浮点数的大小超出了定点机的存储字长

浮点四则运算-溢出判断

最值的计算方法参考 [浮点数的范围计算](#2. 浮点数的表示范围)